Magnonic crystals
When the material parameters or shape of the magnetic sample are periodically modulated in space then the spin wave propagation is significantly altered. These periodic structures are called magnonic crystals. The term crystal is referring to the periodicity of the system which is a distinctive feature of ordered solids where the atoms are periodically arranged in space. This ordering is manifested macroscopically by the regular shape of the crystallites.
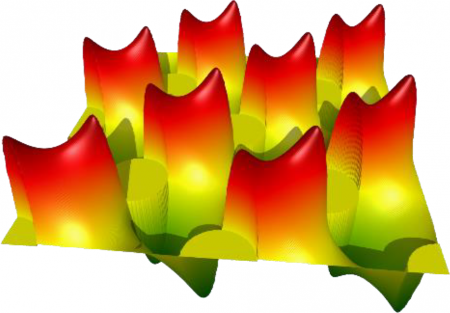
However, the equally important property of the crystals is their anisotropy. The considered artificial magnetic structures, called magnonic crystals, exhibit the anisotropy of magnetic properties. It means, that the spin waves propagate with different velocities in different directions. This allows shaping the propagation of the signal by controlling the spin wave refraction. The wave propagation in periodic structures can be even forbidden in specific ranges of the frequencies due to the destructive interference of scattered waves. This effect described by Lawrence Bragg in atomic crystals is also observed for spin waves in magnonics crystals.
All information about the temporal changes and spatial distribution of waves in linear regime is included in the dependence of the frequency on the wave vector, called the wave dispersion relation. Therefore the main objective in the studies of wave dynamic is the determination of this characteristic and the accompanying spatial profiles of so-called eigenmodes for given values of the wave vector. The dispersion relation for (magnonic) crystal is periodic in the space of the wave vector therefore it needs to determined only in the limited space called the first Brillion zone.
- M. Krawczyk, D. Grundler, Review and prospects of magnonic crystals and devices with reprogrammable band structure, J. Phys.: Cond. Matt., 26, 123202 (2014). DOI: 10.1088/0953-8984/26/12/123202
Planar magnonic crystals
In our studies, we focused on planar magnonic crystals i.e. the structures formed from the magnetic film by the periodic patterning. The characteristic in-plane sizes of considered structures are in the range of single hundreds of nanometers, whereas the thicknesses of magnetic films are about a few tens of nanometers. The pattern can be periodic in one dimension (stipes) or in two dimensions (array of dots), therefore we can consider so-called 1D or 2D magnonic crystals. In this range of sizes, the interplay between classical magnetic dipolar interaction and quantum exchange interaction takes place. Therefore, the physics of the considered systems is reacher and much more complex than for other counterparts of magnonic crystals, such as photonic crystals (operating on light) and phonics crystals (processing the sound or elastic waves).
The interesting feature of magnonic crystals is that the propagating spin waves perceive the geometry of the system indirectly, i.e. by the internal magnetic field produced to by the structure. The internal field can be tuned by the change the direction of the external magnetic field. So, the landscape, in which the spin waves are propagating, has usually of lower symmetry than the structure itself and can be shaped by external biases.
Our research:
- calculations of the dispersion relation of magnonic antidote lattices and antidote waveguides,
- simulation of the Brillouin light scattering dispersion and ferromagnetic resonance spectra,
- analysis of the spin wave edge modes around antidotes,
- studies on the impact of the lattice symmetry, anisotopic structure scaling, and shape of the inclusions on the spin wave spectum in bicomponent magnonic crystals.
- J. W. Kłos, M. L. Sokolovskyy, S. Mamica, M. Krawczyk, The impact of the lattice symmetry and the inclusion shape on the spectrum of 2D magnonic crystals, J. Appl. Phys. 111 , 123910 (2012), DOI: 10.1063/1.4729559
- J. W. Kłos, D Kumar, M Krawczyk, A Barman, Influence of structural changes in a periodic antidot waveguide on the spin-wave spectra, Phys. Rev. B 89, 014406 (2014), DOI: 10.1103/PhysRevB.89.014406
- S. Tacchi, P. Gruszecki, M. Madami, G. Carlotti, J. W. Kłos, M. Krawczyk, A. Adeyeye, G. Gubbiotti, Universal dependence of the spin wave band structure on the geometrical characteristics of two-dimensional magnonic crystals, Sci Rep 5, 10367 (2015). DOI: 10.1038/srep10367
- S. Mamica, M. Krawczyk, D. Grundler, Nonuniform Spin-Wave Softening in Two-Dimensional Magnonic Crystals as a Tool for Opening Omnidirectional Magnonic Band Gaps, Phys. Rev. Applied 11, 054011 (2019), DOI: 10.1103/PhysRevApplied.11.054011
3D magnonic crystals
Three dimensional (3D) magnonic crystals (MCs) are characterized by fully 3D periodic distribution of inclusions. Since both materials (inclusions and matrix) should be magnetic and the lateral size of inclusions is in the range of tens of nanometres the fabrication of such structures is rather tough task. However, there are some promising techniques, such as magnetoferritine crystallization, which uses self-assembling bio-mimetic nanoparticles to form 3D periodic structures as large as hundreds of micrometres. On the other hand, properties of the 3D version of MCs are more complex and richer, and thus worth of investigations.
Our theoretical studies of 3D MCs are devoted mostly to the investigation of possibilities of the magnonic band gaps opening. We explain, e.g., the existence of some threshold of magnetic contrast between constituent materials below which the gap could not open, as well as its relation to the crystallographic structure of the crystal (see Fig.). We also have shown that a proper choice of the MC structure and its filling fraction allows to design an anisotropic and strongly wave-vector-dependent effective damping.
- M. Krawczyk, J. Kłos, M. L. Sokolovskyy, and S. Mamica, Materials optimization of the magnonic gap in three-dimensional magnonic crystals with spheres in hexagonal structure, J. Appl. Phys. 108, 093909 (2010), DOI: 10.1063/1.3501113
- S. Mamica, M. Krawczyk, M. L. Sokolovskyy, and J. Romero-Vivas, Large magnonic band gaps and spectra evolution in three-dimensional magnonic crystals based on magnetoferritin nanoparticles, Phys. Rev. B 86, 144402 (2012), DOI: 10.1103/PhysRevB.86.144402
- J. Romero-Vivas, S. Mamica, M. Krawczyk, and V.V. Kruglyak, Investigation of spin wave damping in three-dimensional magnonic crystals using the plane wave method, Phys. Rev. B 86, 144417 (2012), DOI: 10.1103/PhysRevB.86.144417
Magnonic quasicrystals
The long-range order can have a more general form than periodic arranging. The coherent Bragg scattering of waves leading to the appearance of forbidden ranges of frequencies is also observed in quasicrystals. We investigated the fractal spin wave spectra and self-similar spin wave profiles in bi-component planar magnonic quasicrystals. Particular attention was paid to the bulk localization of spin waves.
Our research:
- calculations of IDOS and fractal dimension of the spectrum of spin wave eigenmodes in bi-component, planar magnonic quasicrystal,
- analysis of the localization of spin wave bulk modes and surface modes in bi-component planar magnonic quasicrystal.
- J. Rychły, J. W. Kłos, M. Mruczkiewicz, M. Krawczyk, Spin waves in one-dimensional bicomponent magnonic quasicrystals, Phys. Rev. B 92, 054414 (2015), DOI: 10.1103/PhysRevB.92.054414
- J. Rychły, S. Mieszczak, J.W. Kłos, Spin waves in planar quasicrystal of Penrose tiling, J. Magn. Magn. Mater. 450, 18 (2018), DOI:10.1016/j.jmmm.2017.03.029
- F. Lisiecki, J. Rychły, P. Kuświk, H. Głowiński, J.W. Kłos, F. Groß, I. Bykova, M. Weigand, M. Zelent, E. J. Goering, G. Schütz, G. Gubbiotti, M. Krawczyk, F. Stobiecki, J. Dubowik, J. Gräfe, Reprogrammability and scalability of magnonic fibonacci quasicrystals, Phys. Rev. Applied 11, 054003 (2019), DOI: 10.1103/PhysRevApplied.11.054003
Magnonic surface states and spin wave localization
The waves in a periodic medium, so-called Bloch waves, cannot propagate in the unconstrained periodic medium when their frequencies are in one of the forbidden ranges. It results from the exponential increase/decrees of their amplitude in this frequency regions. When the periodic structure is terminated and interfaced with homogeneous medium or other periodic structure then exponentially decaying surface states or interface states can exist being localized at the surface/interface. This property is a general one and is valid also for magnonic crystals.
Except the localization related to the interplay between band properties of periodic structure(s) and the perturbation introduced by the surface (interface), we investigated also the other, generic mechanisms of localization, related to the interplay between oscillatory and evanescent solutions in magnonics structure of spatially depended internal demagnetizing field or saturation magnetization.
Our research:
- calculation of localized spin wave modes on the interface two magnonic crystals in exchange regime,
- studies of spin wave surface states in 1D plane magnonics crystal in dipolar and exchange regime,
- investigation of spin wave modes in magnonic antidots lattice and spin wave concentration the components of in bi-component magnonic crystal.
- J. W. Kłos, V. S. Tkachenko, Symmetry-related criteria for the occurrence of defect states in magnonic superlattices, J. Appl. Phys. 113, 133907 (2013), DOI:10.1063/1.4798607
- J. Rychły, J. W. Kłos, Spin wave surface states in 1D planar magnonic crystals, J. Phys. D: Appl, Phys. 50, 164004 (2017), DOI: 10.1088/1361-6463/aa5ae1
Spin waves and interactions
The typical frequencies of spin waves are in the range of GHz which ensures the relatively strong coupling of microwave electromagnetic field with the stray field of spin waves. Therefore one of the most common methods of excitation and detection of spin waves is the usage of microwave cavities of microwave coplanar waveguides. The latter approach is of particular importance for the investigation of spin wave transmission in planar magnonic nanostructures. To excite (and detect) the spin wave effectively, the spatial profile of the microwave field must be matched to the wavenumber of the spin waves. In our studies, we designed coplanar waveguide antennas of changed width which can excite the spin waves locally and generate spin wave beams which can be then used to investigate the spin wave refraction effects.
Some magnetic materials exhibit magnetostrictive properties. However, the coupling between elastic wave and spin waves is weak and difficult to observe even though the frequencies and the wavelength of both excitations can be matched. The main difficulty is the anisotropy of magnetoelastic interaction which requires the careful selection of the direction of a static magnetic field to observe the interaction between spin waves and a particular kind of surface acoustic waves. We investigated the interaction between the spin waves in magnetostrictive layer deposited on elastic substrate and surface acoustic waves concentrated at the surface of this composed system. Our studies explain the peculiarities of magnetoelastic interaction in the thermally generated and elastically exited magnonic crystal (by transient grating technique) by analyzing its magnetic response (using time resolve magnetooptical Kerr effect).
We provided also the numerical model describing the magnetoelastic interaction between thermally exited magnons and phonons in magnetic multilayers which was able to reproduce the result of Brillouin light scattering meassurments.
Our research:
- designing of the coplanar waveguide antennas for the generation of spin wave beams,
- estimation of TR-MOKE response for thermally induced magnonic crystal
- calculations of magnetoelastic dispersion relation for interacting spin waves and surface scoustic waves
- P. Gruszecki, M. Kasprzak, A. E. Serebryannikov, M. Krawczyk and W. Śmigaj, Microwave excitation of spin wave beams in thin ferromagnetic films, Sci. Rep. 6, 22367 (2016), DOI: 10.1038/srep22367
- C. L. Chang, S. Mieszczak, M. Zelent, V. Besse, U. Martens, R. R. Tamming, J. Janusonis, P. Graczyk, M. Münzenberg, J. W. Kłos, R. I. Tobey, Driving magnetization dynamics in an on-demand magnonic crystal via the magnetoelastic interactions, Phys. Rev. Applied 10, 064051 (2018), DOI:10.1103/PhysRevApplied.10.064051
- N. K. P. Babu, A. Trzaskowska, P. Graczyk, G. Centała, S. Mieszczak, H. Głowiński, M. Zdunek, S. Mielcarek, J. W. Kłos, The Interaction between Surface Acoustic Waves and Spin Waves: The Role of Anisotropy and Spatial Profiles of the Modes, Nano Lett. 21, 946 (2021), DOI:10.1021/acs.nanolett.0c03692

