Spin waves in nanotextures
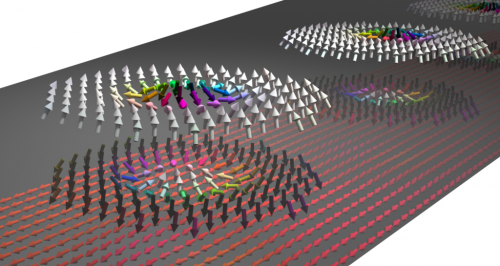
Spin waves are promising carriers for energy-saving, miniaturized and fast microwave signal-processing devices. Our research focuses on developing the physical foundations for future magnonic technologies.
Spin waves are waves of coherently oscillating magnetic moments. Their frequencies are in a microwave range and their wavelengths can be as short as tens of nanometers. Our research is focused on developing the physical foundations for future magnonic technology, which promises to advance energy-saving, miniaturized, and fast signal-processing devices.
Using micromagnetic simulations and developed analytical models, in collaboration with the experimental groups, we are studying the spin-wave dynamics and magnetization dynamics in nanoscopic ferromagnetic systems. Currently, we focus on nonreciprocity in spin-wave dynamics, spin-wave dynamics in complex magnetization textures, like domain walls and skyrmions, control of the spin-wave phase, and coupling between the waves.
Nonreciprocity and coupling
Nonreciprocity is an intriguing property directly related to the time-reversal symmetry breaking. The magnetization dynamics and spin waves are inextricably linked with this property. The main example is a spin wave propagating in thin ferromagnetic film along direction perpendicular to the static magnetization. This type of waves are called magnetostatic surface spin waves or Damen-Eshbach wave. Dzyaloshinskii–Moriya interaction (DMI) also introduces nonreciprocity to spin-wave dynamics. Two sources of the nonreciprocity and chiral magnetostatic elements between ferromagnetic elements open broad range of potential applications.
Our research:
- Study the influence of the nonreciprocal properties on spin-wave dynamics.
- Exploitation of the Dzialoshinky-Moryia and magnetostatic induced nonreciprocity.
- Exploitation of the coupling between waves for magnonic applications.
- K. Szulc, P. Graczyk, M. Mruczkiewicz, G. Gubbiotti, and M. Krawczyk,
Spin-wave diode and circulator based on unidirectional coupling,
Phys. Rev. Applied 14, 034063 (2020). DOI:10.1103/PhysRevApplied.14.034063 - P. Graczyk, M. Krawczyk, S. Dhuey, W.G. Yang, H. Schmidt, and G. Gubbiotti, Magnonic band gap and mode hybridization in continuous permalloy films induced by vertical dynamic coupling with an array of permalloy ellipses,
Phys. Rev. B 98, 174420 (2018). DOI: 10.1103/PhysRevB.98.174420 - P. Graczyk, M. Zelent, and M. Krawczyk,
Co- and contra-directional vertical coupling between ferromagnetic layers with grating for short-wavelength spin wave generation,
New J. Phys. 20, 053021 (2018). DOI: 10.1088/1367-2630/aabb48 - M. Mruczkiewicz, P. Graczyk, P. Lupo, A. Adeyeye, G. Gubbiotti, M. Krawczyk,
Spin wave nonreciprocity and magnonic band structure in thin permalloy film induced by dynamical coupling with an array of Ni stripes,
Phys. Rev. B 96, 104411 (2017). DOI: 10.1103/PhysRevB.96.104411 - P. Graczyk and M. Krawczyk,
Coupled-mode theory for the interaction between acoustic waves and spin waves in magnonic-phononic crystals: Propagating magnetoelastic waves,
Phys. Rev. B 96, 024407 (2017). DOI: 10.1103/PhysRevB.96.024407 - P. Graczyk, J. W. Kłos, and M. Krawczyk,
Broadband magnetoelastic coupling in magnonic-phononic crystals for high-frequency nanoscale spin-wave generation,
Phys. Rev. B 95, 104425 (2017). DOI: 10.1103/PhysRevB.95.104425
Skyrmions, votices and complex magnetization textures
Magnetic skyrmions are topologically protected nanoscale spin textures, which can be regarded as quasi-particles due to their non-trivial topological nature. They become a hot topic in the field of condensed matter physics as they can be used for building future spintronic applications. However, in order to realize skyrmion-based applications, it is important to study the skyrmion dynamics driven by external forces, such as the spin waves and spin current. We investigate stability and full spectrum of eigen-oscillations in the skyrmions of Bloch and Neel type in the nanodots.
The domain walls of both types can scatter but also guide the spin waves. We study interaction between domain walls, of Bloch, Neel or complex type, with the spin waves.
Magnetic vortex is another type of topologically protected magnetic texture having very interesting properties. Its existence is related to the competition of short-range exchange and long-range dipolar interactions. The in-plane vortex, in which all the magnetic moments are aligned in one plane, can have two opposite chiralities of the in-plane magnetization. Additionally, core vortices can present two opposite polarities of the vortex core, i.e. the region around the vortex centre with a nonzero magnetization component perpendicular to the vortex plane. Both the chirality and the core polarity can be switched being the natural candidates for a bit of information. The switching is usually assisted by spin-wave excitations which have a significant influence on the stability of the magnetic configuration as well. In our studies we examined both the frequencies and profiles of the spin waves corresponding to different magnetic states.
Our research:
- Study stability of the skyrmion in confined geometries.
- Description of the excitation spectra of skyrmions.
- Numerical simulation of the interaction between the skyrmion and propagating spin waves.
- Explanation of the spin-wave dynamics in the ferromagnetic film with the domains and domain walls.
- X. Li, L. Shen, Y. Bai, J. Wang, X. Zhang, J. Xia, M. Ezawa, O. A. Tretiakov, X. Xu, M. Mruczkiewicz, M. Krawczyk, Y. Xu, R. F. L. Evans, R. W. Chantrell, and Y. Zhou, Bimeron clusters in chiral antiferromagnets,
npj Comput.Mater. 6, 169 (2020). DOI: 10.1038/s41524-020-00435-y - P. Gruszecki, C. Banerjee, M. Mruczkiewicz, O. Hellwig, A. Barman, and M. Krawczyk, The influence of the internal domain wall structure on spin wave band structure in periodic magnetic stripe domain patterns, Solid State Phys. 70, 79 (2019). DOI: 10.1016/bs.ssp.2019.09.003
- S. Saha, M. Zelent, S. Finizio, M. Mruczkiewicz, S. Tacchi, A. K. Suszka, S. Wintz, N. S. Bingham, J. Raabe, M. Krawczyk, and L. J. Heyderman, Formation of Néel-type skyrmions in an antidot lattice with perpendicular magnetic anisotropy, Phys. Rev. B 100, 144435 (2019).DOI: 10.1103/PhysRevB.100.144435
- K. Szulc, F. Lisiecki, A. Makarov, M. Zelent,1 P. Kuswik, H. Głowinski, J. W. Kłos, M. Münzenberg, R. Gieniusz, J. Dubowik, F. Stobiecki, and M. Krawczyk, Remagnetization in arrays of ferromagnetic nanostripes with periodic and quasiperiodic order, Phys. Rev. B 99, 064412 (2019). DOI: 10.1103/PhysRevB.99.064412
- M. Mruczkiewicz, P. Gruszecki, M. Krawczyk, and K. Y. Guslienko, Azimuthal spin-wave excitations in magnetic nanodots over the soliton background: Vortex, Bloch, and Néel-like skyrmions, Phys. Rev. B 97, 064418 (2018). DOI: 10.1103/PhysRevB.97.064418
- M. Zelent, J. Tóbik, M. Krawczyk, K. Y. Guslienko, M. Mruczkiewicz, Bi-stability of magnetic skyrmions in ultrathin multilayer nanodots induced by magnetostatic interaction, Phys. Stat. Sol. – RRL 11, 1700259 (2017). DOI: 10.1002/pssr.201700259
- C. Banerjee, P. Gruszecki, J. W. Klos, O. Hellwig, M. Krawczyk, and A. Barman, Magnonic band structure in a Co/Pd stripe domain system investigated by Brillouin light scattering and micromagnetic simulations, Phys. Rev. B 96, 024421 (2017). DOI: 10.1103/PhysRevB.96.024421
- M. Mruczkiewicz, M. Krawczyk, and K. Y. Guslienko,
Spin excitation spectrum in a magnetic nanodot with continuous transitions between the vortex, Bloch-type skyrmion, and N´eel-type skyrmion states, Phys. Rev. B 95, 094414 (2017). DOI: 10.1103/PhysRevB.95.094414 - S. Mamica, J.-C. S. Lévy, and M. Krawczyk, Effects of the competition between the exchange and dipolar interactions in the spin-wave spectrum of two-dimensional circularly magnetized nanodots, J. Phys. D 47, 015003 (2014). DOI: 10.1088/0022-3727/47/1/015003
- S. Mamica, J.-C. S. Lévy, Ph. Depondt, and M. Krawczyk, The effect of the single-spin defect on the stability of the in-plane vortex state in 2D magnetic nanodots, J. Nanopart. Res. 13, 6075 (2011). DOI: 10.1007/s11051-011-0308-0
- S. Mamica, J.-C. S. Lévy, M. Krawczyk, and Ph. Depondt, Stability of the Landau state in square two-dimensional magnetic nanorings, J. Appl. Phys. 112, 043901 (2012). DOI: 10.1063/1.4745875
Control of the spin-wave phase
Phase is the one of the most important properties of the waves. Controlling the phase allows to code information in the guiding waves, determines the resonance conditions and the wave interference. To use the spin waves for signal transmission, routing and processing, design meta-lens and meta-antennas the efficient ways of the spin wave phase steering need to be developed.
Our research:
- Developing of the Fabry-Perot and Gires–Tournois interferometers for spin waves in ferromagnetic films.
- Design of the magnonic metasurfaces for applications.
- Focusing of the spin waves.
- Nanoscale control of the spin-wave phase.
- K. Sobucki, W. Śmigaj, J. Rychły, M. Krawczyk, and P. Gruszecki,
Resonant subwavelength control of the phase of spin waves reflected from a Gires–Tournois interferometer,
Sci Rep 11, 4428 (2021). DOI: 10.1038/s41598-021-83307-9 - S. Mieszczak, O. Busel, P. Gruszecki, A. N. Kuchko, J. W. Kłos, and M. Krawczyk, Anomalous refraction of spin waves as a way to guide signals in curved magnonic multimode waveguides, Phys. Rev. Applied 13, 054038 (2020). DOI: 10.1103/PhysRevApplied.13.054038
- Oleksandr V. Dobrovolskiy, Roland Sachser, Sergey A. Bunyaev, David Navas, Volodymyr M. Bevz, Mateusz Zelent, Wojciech Śmigaj, Justyna Rychły, Maciej Krawczyk, Ruslan V. Vovk, Michael Huth, and Gleb N. Kakazei, Spin-wave phase inverter upon a single nanodefect, ACS Appl. Mater. Interfaces 11, 17654−17662 (2019). DOI: 10.1021/acsami.9b02717
- M. Mailian, O.Y. Gorobets, Y.I. Gorobets, M. Zelent, M. Krawczyk,
Exchange spin waves transmission through the interface between two antiferromagnetically coupled ferromagnetic media, J. Magn. Magn. Mater. 484, 484 (2019). DOI: 10.1016/j.jmmm.2019.02.062
Spin-wave optics
Basic equations describing propagation of spin waves differ from those for electromagnetic and acoustic waves. So, the question is, if the phenomena known for electromagnetic or acoustic waves invoke a solution of the Landau-Lifshitz equation. This consists an area of the spin-wave optics. Some of them can be very useful for magnonic applications.
Our research:
- Spin-wave beams and related physics: Goos-Heanchen effect, mirage effect.
- Interference and diffraction effects for spin waves.
- Exploitation of the spin-wave optics for applications.
- F. Groß, M. Zelent, N. Träger, J. Förster, U. T. Sanli, R. Sauter, M. Decker, C. H. Back, M. Weigand, K. Keskinbora, G. Schütz, M. Krawczyk, and J. Gräfe,
Building blocks for magnon optics: emission and conversion of short spin waves, ACS NANO 14, 17184 (2020), DOI: 10.1021/acsnano.0c07076 - M. Gołębiewski, P. Gruszecki, M. Krawczyk and A. Serebryannikov,
Spin-wave Talbot effect in a thin ferromagnetic film,
Phys. Rev. B 102, 134402 (2020). DOI: 10.1103/PhysRevB.102.134402 - J. Gräfe, P. Gruszecki, M. Zelent, M. Decker, K. Keskinbora, M. Noske, P. Gawronski, H. Stoll, M. Weigand, M. Krawczyk, C. H. Back, E. J. Goering, and G. Schütz, Direct observation of spin-wave focusing by a Fresnel lens,
Phys. Rev. B 102, 024420 (2020). DOI: 10.1103/PhysRevB.102.024420 - M. Zelent, M. Mailyan, V. Vashistha, P. Gruszecki, O. Y. Gorobets, Y. I. Gorobets, and M. Krawczyk, Spin wave collimation using a flat metasurface, Nanoscale 11, 9743 (2019). DOI: 10.1039/c8nr10484k
- P. Gruszecki and M. Krawczyk,
Spin-wave beam propagation in ferromagnetic thin films with graded refractive index: Mirage effect and prospective applications,
Phys. Rev. B 97, 094424 (2018). DOI: 10.1103/PhysRevB.97.094424 - M. Mailyan, P. Gruszecki, O. Gorobets, and M. Krawczyk,
Goos-Hänchen shift of a spin-wave beam at the interface between two ferromagnets, IEEE Trans. Magn. 53, 7100605 (2017). DOI: 10.1109/TMAG.2017.2696581
Excitation of spin waves
The spin waves span a broad range of frequencies from few to hundreds of GHz with respective wavelengths from the range of few micrometers down to tens of nanometers. Excitation of long-wavelength waves is nowadays a routine process with the use of the inductive methods. However, for the excitation of the short-wavelength, i.e., below 100 nm spin waves, or excitation of the spin-wave beams new approaches are required.
Our research:
- Looking for local source of propagating spin waves.
- Developing concepts for short-wavelength spin-wave excitation.
- N. Träger, F. Lisiecki, R. Lawitzki, M. Weigand, H. Głowinski, G. Schütz, G. Schmitz, P. Kuswik, M. Krawczyk, J. Gräfe, and P. Gruszecki,
Competing spin wave emission mechanisms revealed by time-resolved x-ray microscopy,
Phys. Rev. B 103, 014430 (2021), DOI: 10.1103/PhysRevB.103.014430 - P. Gruszecki, I. L. Lyubchanskii, K. Y. Guslienko, and M. Krawczyk,
Local non-linear excitation of sub-100 nm bulk-type spin waves by edge-localized spin waves in magnetic films,
Appl. Phys. Lett. 118, 062408 (2021); DOI: 10.1063/5.0041030
Nonlinear effects
Nonlinearity is a inherent property of magnetic materials, remagnetization processes and magnetization dynamics. At the same time it is an indispensable property to use waves for signal processing, self-synchronization, amplification or magnetization reconfiguration.
Our research:
- Dynamic formation of the magnetization pattern.
- Inelastic spin-wave scattering processes.
- Space-time magnonic crystals
- Excitation of short-wavelength spin waves.
- P. Gruszecki, I. L. Lyubchanskii, K. Y. Guslienko, and M. Krawczyk,
Local non-linear excitation of sub-100 nm bulk-type spin waves by edge-localized spin waves in magnetic films, Appl. Phys. Lett. 118, 062408 (2021); DOI: 10.1063/5.0041030 - N. Träger, P. Gruszecki, F. Lisiecki, F. Groß, J. Förster, M. Weigand, H. Głowiński, P. Kuświk, J. Dubowik, G. Schütz, M. Krawczyk, and J. Gräfe,
Real-space observation of magnon interaction with driven space-time crystals, Phys. Rev. Lett. 126, 057201 (2021); DOI: 10.1103/PhysRevLett.126.057201
Synopsis: Making Space-Time Crystals Using Magnons, Physics – Making Space-Time Crystals Using Magnons (aps.org) - N. N. Dadoenkova, Y. S. Dadoenkova, I. L. Lyubchanskii, M. Krawczyk, and K. Y. Guslienko, Inelastic spin-wave scattering by Bloch domain wall flexure oscillations, Phys. Status. Solidi RRL 2019, 1800589 (2019). DOI: 10.1002/pssr.201800589
- Y. Dadoenkova, N. Dadoenkova, M. Krawczyk, and I. Lyubchanskii,
Goos–Hänchen effect for Brillouin light scattering by acoustic phonons,
Opt. Lett. 43, 3965 (2018). DOI: 10.1364/OL.43.003965
Spin waves in confined geometry
Exploitation of the spin-wave dynamics in nanoscale requires deep knowledge on the magnetization configuration and spin-wave spectra in confined geometries.
Our research:
- Numerical simulation of the remagnetization process.
- Calculation of the spin wave spectra.
- N. Träger, P. Gruszecki, F. Lisiecki, J. Förster, M. Weigand, S. Wintz, H. Stoll, H. Głowinski, P. Kuswik, M. Krawczyk, and J. Gräfe,
Direct imaging of high-frequency multimode spin wave propagation in cobalt-iron waveguides using X-ray microscopy beyond 10 GHz,
Phys. Status Solidi – RRL 2020, 2000373 (2020). DOI: 10.1002/pssr.202000373 - O. V. Dobrovolskiy, S. A. Bunyaev, N. R. Vovk, D. Navas, P. Gruszecki, M. Krawczyk, R. Sachser, M. Huth, A. V. Chumak, K. Y. Guslienko, and G. N. Kakazei, Spin-wave spectroscopy of individual ferromagnetic nanodisks,
Nanoscale 12, 21207 (2020). DOI: 10.1039/D0NR07015G - N. Träger, P. Gruszecki, F. Lisiecki, F. Groß, J. Förster, M. Weigand, H. Głowiński, P. Kuświk, J. Dubowik, M. Krawczyk, and J. Gräfe,
Demonstration of k-vector selective microscopy for nanoscale mapping of higher order spin wave modes, Nanoscale 12, 17238 (2020). DOI: 10.1039/d0nr02132f - S. Pan, S. Mondal, M. Zelent, R. Szwierz, S. Pal, O. Hellwig, M. Krawczyk, and A. Barman, Edge localization of spin waves in antidot multilayers with perpendicular magnetic anisotropy, Phys. Rev. B 101, 014403 (2020). DOI: 10.1103/PhysRevB.101.014403
- Julia Kharlan, Pavlo Bondarenko, Maciej Krawczyk, Olga Salyuk, Elena Tartakovskaya, Aleksandra Trzaskowska, and Vladimir Golub,
Standing spin waves in perpendicularly magnetized triangular dots,
Physical Review B 100, 184416 (2019). DOI: 10.1103/PhysRevB.100.184416 - J. Rychły, V. S. Tkachenko, J. W. Kłos, A. Kuchko, and M. Krawczyk,
Spin wave modes in a cylindrical nanowire in crossover dipolar-exchange regime, J. Phys. D: Appl. Phys. 52, 075003 (2019). DOI: 10.1088/1361-6463/aaf2fc - S. Mamica, X. Zhou, A. Adeyeye, M. Krawczyk, and G. Gubbiotti,
Spin-wave dynamics in artificial anti-spin-ice systems: Experimental and theoretical investigations, Phys. Rev. B 98, 054405 (2018). DOI: 10.1103/PhysRevB.98.054405 - O. Busel, M. Zelent, O. Gorobets, Y. Gorobets and M. Krawczyk,
The resonant dynamic magnetization distribution in ferromagnetic thin film with the antidot, Acta Phys. Pol. A 133, 492 (2018). DOI: 10.12693/APhysPolA.133.492

